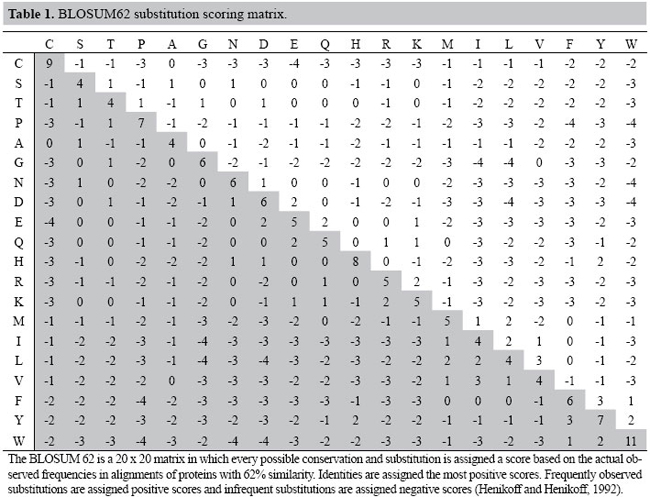
A simple genetic algorithm for multiple sequence alignment C. Gondro and B.P. Kinghorn Genet. Mol. Res. 6 (4): 964-982 (2007) ABSTRACT. Multiple sequence alignment plays an important role in molecular sequence analysis. An alignment is the arrangement of two (pairwise alignment) or more (multiple alignment) sequences of ‘residues’ (nucleotides or amino acids) that maximizes the similarities between them. Algorithmically, the problem consists of opening and extending gaps in the sequences to maximize an objective function (measurement of similarity). A simple genetic algorithm was developed and implemented in the software MSA-GA. Genetic algorithms, a class of evolutionary algorithms, are well suited for problems of this nature since residues and gaps are discrete units. An evolutionary algorithm cannot compete in terms of speed with progressive alignment methods but it has the advantage of being able to correct for initially misaligned sequences; which is not possible with the progressive method. This was shown using the BaliBase benchmark, where Clustal-W alignments were used to seed the initial population in MSA-GA, improving outcome. Alignment scoring functions still constitute an open field of research, and it is important to develop methods that simplify the testing of new functions. A general evolutionary framework for testing and implementing different scoring functions was developed. The results show that a simple genetic algorithm is capable of optimizing an alignment without the need of the excessively complex operators used in prior study. The clear distinction between objective function and genetic algorithms used in MSA-GA makes extending and/or replacing objective functions a trivial task. Key words: Genetic algorithms, Evolutionary computation, Optimization, Multiple sequence alignment INTRODUCTION Multiple sequence alignment (MSA) is an important part of molecular sequence analysis which is routinely used to identify and measure similarities between samples of DNA, RNA or protein. An alignment is the arrangement of two or more sequences of ‘residues’ (nucleotides or amino acids) that maximizes the similarities between them. It can be pivotal in the reconstruction of phylogenetic trees or an important tool in the prediction of the function and/or structure of an unknown protein by aligning its sequence with others of known function and/or structure. A third use is the prediction of probes for the same family of sequences in the same or different organisms. The relationships between sequences are very complex since they have been exposed to evolutionary pressures and mutations over millions of years. Obviously, the best way to infer these relationships would be from a solid knowledge of the evolutionary history and the structural properties of the sequences. Unfortunately, this wealth of information is very seldom available; instead, generic models of protein evolution based on sequence similarity are used (Henikoff and Henikoff, 1992) in a scoring system which penalizes substitutions and gap insertions. The highest scoring alignment can be found through a dynamic programming (DP) algorithm such as the Needleman-Wunsch (1970) or Smith-Waterman (1981). However, these algorithms are computationally demanding in all but the most trivial problems. To circumvent this limitation, most multiple alignment methods implement approximate heuristic algorithms. Currently, the main approach to multiple sequence alignment is the progressive method (Feng and Doolittle, 1987) implemented in Clustal W (Thompson et al., 1994), MULTAL (Taylor, 1987) and T-COFFEE (Notredame et al., 2000) for instance. This method is very fast and straightforward but it can easily get caught at local minima. A second method is the exact method, such as MSA (Lipman et al., 1989), which tends to give better results than the progressive method but is computationally too intensive for larger problems; the practical limit is around 10 sequences. The third method is the iteration-based approach. This method uses algorithms that produce an alignment and tries to improve it over successive iterations. This approach includes hidden markov models (Eddy, 1998; Karplus and Hu, 2001), simulated annealing (Kim et al., 1994), tabu search (Riaz et al., 2004), genetic algorithms (Notredame and Higgins, 1996; Zhang and Wong, 1997; Anbarasu et al., 2000; Nguyen et al., 2002; Shyu et al., 2004) and evolutionary programming (Chellapilla and Fogel, 1999). A hybrid method using progressive alignment and iteration was suggested by Thomsen et al. (2002). No single approach is ideal for all scenarios as evidenced by McClure et al. (1994), Wallace et al. (2005) and Thompson et al. (1999a), where the latter evaluated the performance of several alignment programs using the alignments in the BaliBase (Thompson et al., 1999b; Bahr et al., 2001) benchmark as test cases. From the above, it should be clear that the methods and tools for sequence alignment are numerous and there is as yet no optimal approach to the problem. Progressive alignment methods are fast and deterministic, in the sense that they always provide the same result. These are two important considerations for routine applications. Their major problem is that errors in the initial alignments are propagated to the other sequences and cannot be corrected. This is not a problem with iterative methods but they tend to be much slower, and since most are stochastic, results may vary between runs. Iterative methods are well suited for complex problems where no other alternative is available or where the best possible alignment is important irrespective of computational cost. Iterative methods can be implemented through evolutionary algorithms which are computational heuristics that use analogies of natural selection processes such as mutation, recombination and selection to evolve a population of candidate solutions based on an objective function. These algorithms have an important advantage over progressive methods in that the alignment component is independent of the scoring function. This means that different objective functions can be tested without modifications to the alignment routine, which makes them particularly well suited for testing new scoring functions. Also, by their very nature, evolutionary algorithms are easily parallelizable which meets the current trend of low-cost clusters and multi-core processors. This can shift the time-cost balance since parallelization of DP algorithms is not a trivial task (Ebedes and Datta, 2004). This paper describes a simple genetic algorithm (GA) (Goldberg, 1987; Eshelman, 2000), a class of evolutionary algorithms, developed for the MSA of biological sequences. The algorithm was implemented in the software MSA-GA which is freely available from the first author. Two methods are available for creating initial candidate solutions: 1) from pairwise alignments, where sequences are aligned in pairs alone, or 2) from a combination of pairwise alignments and a user-defined multiple sequence alignment. A set of hand-curated alignments from BaliBase (Thompson et al., 1999b; Bahr et al., 2001) were used to compare the alignments produced by the two approaches in MSA-GA with the alignments generated by Clustal W. The remainder of the paper is organized as follows. Background information on sequence alignment and the iterative methods based on evolutionary computation are briefly reviewed. Following this, our genetic algorithm and its implementation in the MSA-GA software is presented. The results of MSA-GA in comparison to alignments of Clustal W are shown and discussed. Conclusions are drawn in the closing section. Sequence alignment A pairwise alignment is the arrangement of two sequences that maximizes the similarities between them. The term similarity refers to the number of matches of residues between the sequences; which is distinct from homology which refers to common evolutionary roots. Sequences that align well are considered homologous; with the distinction between homologous and nonhomologous not clearly distinguishable at around 30% identity - the twilight zone (Sander and Schneider, 1991). The residues in aligned sequences can be a match, a mismatch or a gap. For homologous sequences, a match suggests an evolutionarily conserved region; a mismatch shared between two sequences can indicate derivation from a common ancestor, and a gap is usually explained through insertions or deletions in the sequences. Mismatches and gaps are used to bring as many identical or similar residues into register following a scoring scheme. Alignments can be global or local; the former approach uses the entire sequences to maximize the number of matched residues and the latter approach maximizes the alignment of similar subregions. Multiple sequence alignments are simply an extension of pairwise alignment with three or more sequences. Dynamic programming DP is widely used in optimization problems (Bellman, 2003); it is mathematically guaranteed to find the optimal alignment (Shyu et al., 2004) and is routinely used for pairwise alignments. For three or more sequences the algorithmic complexity grows significantly (Stoye et al., 1997), and since it is a large combinatorial problem (NP-hard) the computational effort becomes prohibitive (Bonizzoni and Della Vedova, 2001; Just, 2001). In a nutshell, DP is a recursive procedure that splits a problem into a set of interdependent sub-problems in which the next intermediate solution is a function of a prior sub-problem and the next solution depends only on its immediate neighbors. For a pairwise alignment problem, DP starts at the end of the sequences and attempts to match all possible pairs of residues according to a scoring scheme for matches, mismatches and gaps generating a matrix of score values for all possible alignments between the two sequences. The highest score identifies an optimal alignment. The score matrix has dimensions n,m - where n and m are the lengths of the two sequences - and is constructed from top to bottom; to reach a given position (i, j) in the matrix from a previous move, there are three possible paths: a diagonal move with no gap penalty from position (i-1, j-1); a move from position (i-1, j) to (i, j), and a move from position (i, j-1) to (i, j) with a gap penalty. The matrix is built recursively according to Equation 1. The actual alignment is obtained from a second matrix, the trace-back matrix - which stores information of the moves through the matrix by backtracking the moves made to obtain the highest score (Durbin et al., 1998).  In equation 1 the function value F(i, j) is the highest score for position i in sequence x and position j in sequence y; d is the cost of the gap penalty, and s is the score for a match/mismatch between residues xi and yj. At position F(0, 0), the value is set to zero. More than one path can lead to the same value and a choice has to be made as to which path to follow. Most programs report a single optimal alignment (Mount, 2004). The choice of scoring scheme and gap penalties influences the alignment produced by the DP algorithm. Progressive alignment Progressive alignment (Feng and Doolittle, 1987) is the most widely used heuristic for aligning multiple sequences, but it is a greedy algorithm that is not guaranteed to be optimal. DP is used to build the multiple alignment which is constructed by aligning pairs of sequences from the most closely related sequences to the furthest apart with the order of alignments defined by a guide tree of edit distances. To build the tree, the pairwise distances between all sequences are calculated and these are used in a phylogenetic method such as neighbor-joining (Saitou and Nei, 1987). The main drawback of progressive alignment is that once a sequence has been aligned it will not be modified again, even if it is suboptimal when other sequences are subsequently aligned. This means that information from more distantly related sequences cannot be used to correct initial misalignments. The approach is most efficient when aligning closely related sequences without outliers and without long insertions or deletions in the sequences (Notredame, 2002). Clustal W (Thompson et al., 1994; Chenna et al., 2003) is the most popular multiple sequence alignment program. It uses a global progressive alignment method. The alignment steps are: 1) pairwise alignment of all sequences using dynamic programming or a fast approximate k-tuple method. 2) The scores of the pairwise alignments are used to build a distance matrix of genetic distances. Initially the number of matched positions divided by the total number of residues without gaps is obtained; these scores are divided by 100 and subtracted from 1.0 to get the actual distances. These are used to build the guide tree using the neighbor-joining method (Saitou and Nei, 1987). 3) Dynamic programming is used to align the sequences from the most closely related to the least closely related guided by the distances from the tree. Scoring systems and objective functions Alongside the local minimum problem due to the greedy nature of the progressive method, Thompson et al. (1994) highlighted the importance of the parameter choice in Clustal W. Iterative methods are equally affected by the choice of parameters which if inadequate will yield false global optima. Thus, a critical step in any MSA is the definition of a relevant scoring system. A scoring system includes scores for matches, mismatches, substitutions, insertions, and deletions. In practical terms it can be split into two components: substitution matrices which provide a numerical score for matches and mismatches, and gap penalties which allow numerical quantification of insertions and deletions. A substitution matrix is a table of numbers of dimension 20 x 20 (see example in Table 1) for amino acids and 4 x 4 for nucleic acids which represents all possible transitions between the 20 amino acids or the 4 nucleic acids. They provide a measure of the probability of a substitution or conservation occurring. Since the direction of a substitution is unknown, the matrices are symmetric. For DNA sequences, a simple matrix commonly used assigns a positive value for a match and a negative value for a mismatch. For protein sequences the most common matrices are percent of accepted mutation (PAM; Dayhoff, 1978) and blocks of amino acid substitution matrices (BLOSUM; Henikoff and Henikoff, 1992). Values in the matrix are commonly given as the log odds score of the substitution occurring (Table 1), with substitutions or conservations more frequent than randomly expected assigned positive values and underrepresented substitutions/conservations assigned negative values. Both types of matrices are followed by a number (PAM250, BLOSUM62) which in the PAM matrices the number refers to the evolutionary distance - a PAM1 matrix estimates the expected substitution rate if 1% of the amino acids changed into any other - this roughly represents a period of 50 million years of evolution. Thus, greater numbers indicate greater distances. In the BLOSUM matrices, the number refers to the minimum percent identity of the blocks used to construct the matrix - in a BLOSUM62 (Table 1) the sequences have a 62% identity. Thus, greater numbers indicate shorter evolutionary distances. BLOSUM is regarded as a preferable matrix choice since each matrix was constructed from actual data while the PAM matrices extrapolate from PAM1 assuming a fixed and independent mutation rate at all sites and over time, while in reality sites vary in their mutability and the rate of mutation over time is also not invariable (George et al., 1990). A further criticism of PAM matrices is the small size of the original dataset. A new set of PAM matrices derived from a large dataset was presented by Jones et al. (1992). Other substitution matrices have been developed such as, for example, the matrices of Gonnet et al. (1992) constructed using data from the entire Swiss protein database, which are currently regarded as being the most accurate.
To obtain the best possible alignment, gaps are introduced in the sequence and a scheme for penalizing these gaps must be adopted. The most common approach is the affine gap penalty model where an initial penalty is used to start a gap and a smaller linear penalty is used for extending the gap an extra position (Equation 2). The assumption of the model is that a single mutation event of x residues is more likely than x adjacent mutations of a single gap; thus, in the alignment there are preferably few longer gaps than a large quantity of short gaps. In Equation 2, the total gap penalty (d) is the penalty of opening a gap (g) plus the cost of extending the gap (r) times the size of the gap (x).
The values of gap penalties depend on the choice of matrix and must balance their values (Altschul, 1989). A high gap penalty in relation to the values in the matrix will impede the appearance of gaps. On the other extreme, a too low gap penalty will cause gaps to appear everywhere in the alignment. Several scoring schemes have been developed. A frequently used scoring scheme is the sum of the score of all pairwise alignments - sum-of-pairs. This approach assumes that the sequences are independent from each other, and there is an overestimation of the number of substitutions. To account for this effect, the sun-of-pair scores, s, over k sequences can be weighted by a factor, w, that accounts for this effect by reducing the influence of the most closely related sequences (Equation 3). Weighted sun-of-pair is used in Clustal W - the W stands for weighted - and are usually obtained from the distances in the guide tree (Thompson et al., 1994).
Other scoring schemes use consistency scores which are a measure of consistency of the MSA with a library of pairwise alignments. This scheme is used in the tree-based consistency based objective function for alignment evaluation - T-COFFEE (Notredame et al., 1998, 2000). In summary, the final MSA is a function of the substitution matrix, gap penalty function, scoring scheme, and optimization algorithm. The first three form the objective function which is condensed into a single numerical value with the scoring scheme. The objective function is the criterion from which the optimization algorithm must try to find the global maximum. Even if the global maximum is found, the alignment is only optimal in the mathematical sense. The true optimal alignment should reflect the actual identity by descent of the components under test which can differ from the mathematical optimum. Multiple sequence alignment with evolutionary computation Progressive methods have the problem of propagating initial misalignments into the entire MSA, which becomes particularly evident in more distantly related sequences (Thompson et al., 1994). Iterative methods try to correct for this problem by iteratively realigning subgroups of the alignments and then aligning them into the entire MSA. With the use of an objective function such as the sum-of-pairs, the aim is to improve the MSA alignment score. Iterative methods can be deterministic or stochastic; here, the discussion is limited to evolutionary computation approaches to MSA, which are stochastic methods. Comprehensive evaluations of iterative algorithms were presented by Hirosawa et al. (1995) and Wallace et al. (2005). Evolutionary computation is the general umbrella for a group of stochastic problem-solving methods loosely inspired by evolutionary processes such as selection, mutation and recombination. These methods are commonly referred to as evolutionary algorithms which have in common the use of populations of candidate solutions which reproduce, compete, and are subjected to selective pressures and random variation - the four basic elements of evolution (Atmar, 1994). The seminal work in the field, SAGA (Notredame and Higgins, 1996), is the best known MSA algorithm using evolutionary computation. SAGA uses a GA with 22 different types of complex search operators that are themselves optimized during runtime using dynamic scheduling. The objective function is the weighted sum-of-pairs. Such complexity may be unnecessary. Thomsen and Boomsma (2004) showed that operator scheduling did not improve the quality of alignments in comparison to a uniform selection of operators, they also showed evidence that crossover operators contributed little to improve alignments, with mutation operators being the main determinant in successful alignments. Zhang and Wong (1997) used a simpler GA but the scoring scheme was based on the number of fully matched columns which limited the algorithm to sequences of high similarity. Evolutionary computation approaches are computationally intensive; to account for this time demand, Anbarasu et al. (2000) developed a parallelized GA based on the island model. A second parallel GA, limited to multi-processor single machines, was presented by Nguyen et al. (2002). Their approach uses a parallelized hybrid GA based on the coarse-grained parallel model. Shyu et al. (2004) used GAs to optimize the guide tree used for progressive alignment methods and also presented a method using a "vertically scalable encoding scheme" for evolving the MSA, which demands approximately the same number of iterations to converge, irrespective of the number of sequences to be aligned. Both methods were only used and evaluated on simulated DNA sequences limiting their practical application. Chellapilla and Fogel (1999) used an evolutionary programming approach with five different variation operators. Their results indicate that their evolutionary programming is more efficient than Clustal W for DNA sequences of low similarity. It should be emphasized that these approaches are slow compared to progressive methods. Speed can be improved by parallelization; another approach that not only improves the speed but also the quality of the alignments is to seed the initial population with pre-alignments, as for example, use the results of Clustal W to form the initial population (Thomsen and Boomsma, 2004) or a hybrid method using progressive alignment and iteration (Thomsen et al., 2002). METHODS A simple genetic algorithm for multiple sequence alignment For simplicity the algorithm is illustrated using DNA sequences, but it can easily be extended to RNA and protein sequences. The software MSA-GA allows alignment of any type of sequence; comparisons with Clustal W were performed using protein sequences which are more challenging due to their structural properties. Matrix representation A group of sequences to be aligned consist of n sequences of DNA of different lengths. An alignment is represented as a matrix with n rows in which each row represents a sequence. Each position in the array is occupied by a symbol from the alphabet {A,T,C,G,-}, with the character symbols corresponding to the nucleotides adenine, thymine, cytosine, and guanine, respectively. Gaps are represented by the symbol ‘-’. Evidently, the order of the nucleotides in the sequences has to be preserved and is only interspaced with gaps. The number of columns in the matrix was defined as
where the number of columns (L) is the size of the longest sequence multiplied by a scaling factor of k plus an initial offset x. An alignment, after gaps have been inserted, is infrequently more than 20% longer than the longest sequence. An adequate scaling factor is in the range {1.2,1.5}. The offset is the maximum number of gaps inserted at the beginning of a sequence. Population initialization Each organism in the GA consists of a candidate alignment. The organisms of the initial population are generated from pairwise alignments of all the sequences. Initially, all global pairwise alignments between the sequences are computed with dynamic programming using the Needleman-Wunsch algorithm (Needleman and Wunsch, 1970). For each sequence one of the pairwise alignments corresponding to that sequence is randomly selected to form the organism. At the beginning of the sequence, a randomly defined number of gaps is placed (offset). The number of gaps is an integer that varies between zero and the size of the offset. Figure 1 summarizes the pseudo-code algorithm for population initialization. Once an organism is constructed, the objective function is called and an initial fitness value is assigned to the organism. Even accounting for the overhead to calculate the pairwise alignments, an initial population seeded from pairwise alignments is overall faster and greatly improves the scores with reduced convergence times when compared to randomly generated alignments (data not shown). With this approach, the initial population starts with a high mean fitness. A second method available in MSA-GA is to include a pre-alignment which is inserted into the initial population.
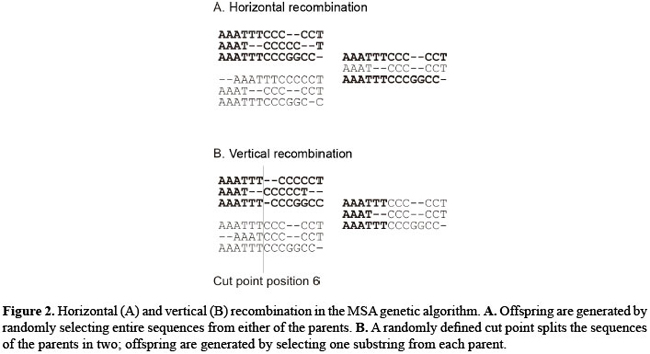
Variation operators An MSA is defined by the position and size of the gaps in the sequences. From an Evolutionary computation perspective it can be viewed as a "gap-shuffling" operation. Two types of search operators were included in the algorithm: recombination between parents to produce offspring alignments and gap mutations. Two types of recombination were adopted with independent probabilities of occurring. Offspring are created by one of the recombination types: 1) horizontal recombination which builds an offspring by randomly selecting each sequence from one of the parents and 2) vertical recombination which randomly defines a cut point in the sequence and the offspring is built by copying the sequence from position 1 up to the cut point from one parent and from the cut point to the end of the sequence from the other parent. The same cut point is used throughout all sequences; initially for each sequence, a new cut point was randomly selected, but this approach proved to be excessively disruptive to the alignments. With vertical recombination, the positions of gaps are accounted for to ensure integrity of the structure of the sequences. Figure 2 exemplifies the two types of recombination. There are no optimal probability settings for the recombinations; empirical observations suggest that an equal chance of either method being selected with a 30% probability for horizontal recombination and 50% for vertical recombination is generally appropriate. If no recombination occurs, the offspring is copied from one of the randomly selected parents.
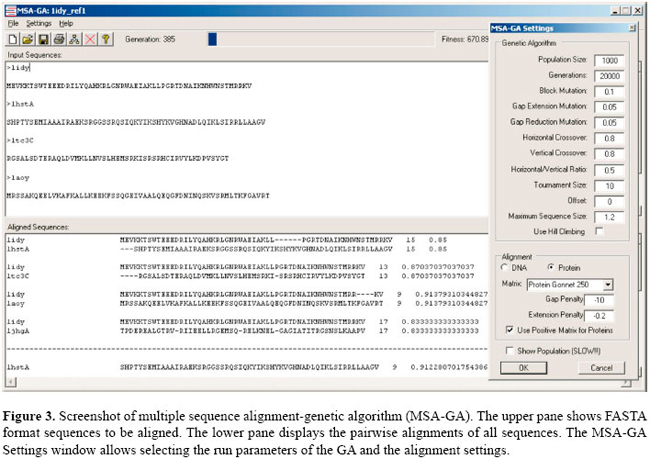
Mutation operators can only act on gaps and there are four possible operations: open a new gap, close an existing gap, extend gap size, or reduce gap size. Three mutation operators were used to manipulate gaps. To open a new gap a block mutation operator is used; a position in a sequence is randomly selected, and a block of gaps of variable size is inserted into the sequence. For gap extension, a block of gaps is randomly selected and an extra gap position is added. The third mutation operator is a gap reduction, a block of gaps is randomly selected and a gap position is removed; the probability of a gap position being removed is an inverse function of the size of the gap, meaning that the smaller the number of gap positions the higher the probability that a gap position will be removed. If the selected gap block consists of a single position, it will always be removed, and the gap will be closed. Hill climbing In MSA-GA, if the best fitness in the population does not improve over 1000 objective function evaluations, an optional greedy hill climbing algorithm (Michalewicz and Fogel, 2000) can be run to try to further improve the alignments. For the best candidate alignment the hill climbing algorithm goes through each block of gaps in each sequence, adds an extra gap position and evaluates the objective function. If the fitness value improves, another gap is added to the block and the fitness is re-evaluated. The process is repeated while the fitness improves. When the new gap results in a worse fitness, the gap is removed and the algorithm moves on to the next block. If the best fitness improves, the GA resumes the run; if not the same process is repeated but deleting a gap position instead of adding one. At the end of the process the GA resumes the run. Objective function The objective function is not an integral part of the GA which makes it particularly well suited for testing different scoring schemes. In our GA, the fitness value is a direct 1:1 mapping of the objective function, meaning that the scores from the objective function are directly assigned as the fitness of the candidate alignment. The objective function used is the weighted sum-of-pairs (Equation 3). In MSA-GA the weights are user-defined and can be derived from the scores of the pairwise alignments used to seed the initial population with the neighbor-joining method (Saitou and Nei, 1987) or some other weighting scheme. Weights are normalized following the method of Thompson et al. (1994). Initial gap opening and gap extension penalties are modified following Thompson et al. (1994). The GA uses steady-state generations and selection is elitist with tournament selection (Bäck et al., 2000). The winner of the tournament remains in the population and the loser(s) are replaced by its (their) offspring. Recombination uses the tournament winner and each of the losers to generate an offspring which will replace the respective loser in the population. If there is no recombination, the winner is used as a template for the mutation operators. Multiple sequence alignment-genetic algorithm software MSA-GA implements the simple GA described. The main drive in the software design was to ensure a clear separation between the GA and the objective function using an object-oriented approach. The GA communicates with the objective function by sending out a candidate alignment as a character matrix of dimension (n, j), where n is the number of sequences in the alignment and j is the maximum number of columns as per equation 4. The objective function returns a numerical score which is the fitness of the candidate alignment. This clear distinction between GA and objective function makes it very simple to implement different objective functions. FASTA format sequences can be pasted directly into the input pane (Figure 3) or read from a file. The GA run parameters can be set in the MSA-GA Settings window (Figure 3). This window also includes settings for the alignment: type of alignment (DNA or protein), where RNA is not included since RNA sequences are usually converted into amino acid sequences for alignments; scoring matrix and initial penalty values for opening and extending gaps. Hill Climbing settings can also be changed (OFF by default). The current version includes the most commonly used scoring matrices; for DNA the identity and Blast matrices and for proteins the main PAM, BLOSUM and GONNET matrices. At the beginning of a run, MSA-GA will automatically search for weights and prealignment files with the same name as the current file. If a weight file is not available, the program will use a default weight of 1.0 for all sequences - unweighted sum-of-pairs. If an alignment file is available, MSA-GA will check its integrity and assign the alignment as the first candidate alignment in the population. On initialization, the lower pane displays the pairwise alignments for all sequences (Figure 3) with the alignment scores and the size of each alignment. At the end of the run, the best alignment is displayed in the same pane. Run results can be saved as text files in FASTA format.
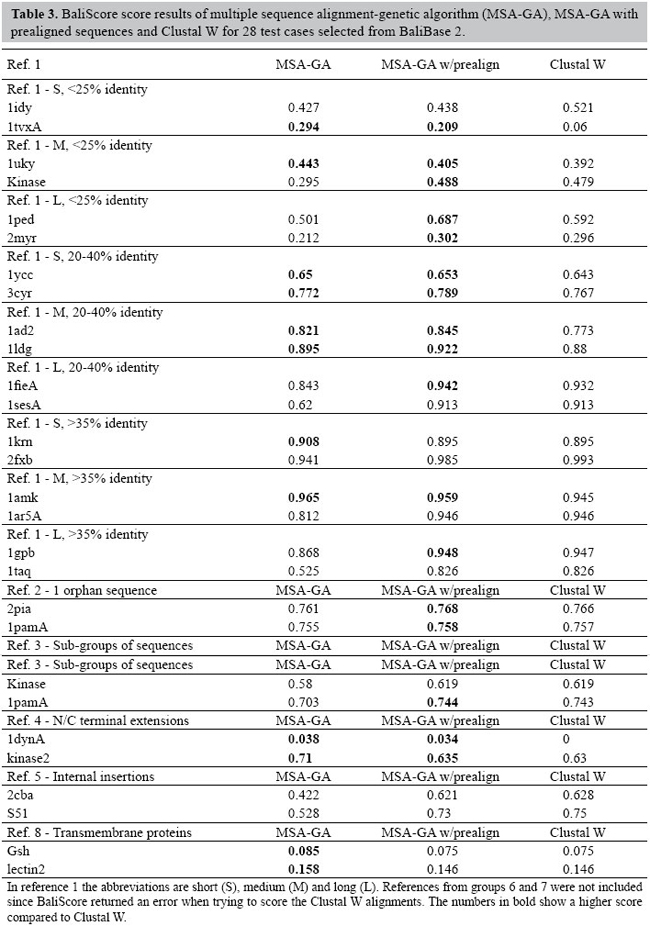
RESULTS Evaluation of MSA-GA for multiple sequence alignment of proteins To evaluate the performance of MSA-GA, a set of test cases from the hand-curated Benchmark Alignment Database - BaliBase (Thompson et al., 1999b; Bahr et al., 2001) was chosen. The original BaliBase (Thompson et al., 1999b) consists of a set of 142 reference alignments with over 1000 sequences. Version 2 of BaliBase (Bahr et al., 2001) improved some alignments from the original database and extended it to 167 reference alignments and over 2100 sequences including sequences with repeated regions, transmembrane sequences and circular permutations. BaliBase 2 is divided into eight classes of reference sets: 1) equidistant sequences with different levels of conservation, 2) sequences with a highly divergent sequence, 3) groups with less than 25% identity, 4) sequences with N/C-terminal extensions, 5) internal insertions, 6) repeats, 7) circular permutations, and 8) transmembrane proteins (Bahr et al., 2001). Group 1 is subdivided by sequence sizes. From each group (and subgroups in group 1), sequences were randomly selected for the test cases, giving a total of 32 as a representative sample of the entire database. This provides a basis for evaluation in which a target result is available for each set of sequences. This result is the outcome of hand-curation, and does not represent the optimal result based on the scoring systems used here. This means that a true global optimization in the tests carried out generally need not to be reflected by complete alignment of the BaliBase solution. Two sets of five runs for each test case were performed using MSA-GA. The parameter settings of the runs are summarized in Table 2, hill climbing was not used since it is very time demanding, and initial tests indicated that hill climbing would improve the GA-evolved alignment less than 1% of the times. For the first set, initial populations were generated using only pairwise alignments. For the second set, pairwise alignments and the alignments from Clustal W were used to seed the initial population. The weights were obtained from the guide trees used in Clustal W. MSA-GA alignments were compared to alignments produced by Clustal W, which is the standard reference alignment program (Chenna et al., 2003). To compare the results with Clustal W, the sum-of-pairs score from BaliScore (Thompson et al., 1999a) was used. BaliScore compares the aligned sequences from BaliBase with an alignment produced by an MSA program and returns an alignment score between zero (bad alignment) and one (good alignment) which can be used to estimate the quality of an alignment in relation to a BaliBase reference, as well as being directly comparable across the different alignment algorithms. Since MSA-GA outputs result in FASTA format, and BaliScore takes MSF formats as inputs, a small graphical wrapper was written to convert from FASTA to MSF using ReadSeq, a common converter of sequence formats, and then a modified version of BaliScore (Thompson J, personal communication) was run with the scores saved as text files. Table 3 shows the score of the best run of MSA-GA for the test cases in comparison to the scores from Clustal W. The default parameters of Clustal W were used to generate the alignments, and the same settings were used in MSA-GA: initial gap opening penalty of 10.0, gap extension penalty of 0.2 and a positive matrix. Instead of the Gonnet series matrix, only the Gonnet 250 matrix was used. BaliScore returned an error when trying to score the Clustal alignments for reference groups 6 and 7. For this reason, the results for these groups were omitted from Table 3.
The average scores for the 28 alignments were 59.04% for MSA-GA, 65.29% for MSA-GA seeded with prealignments and 63.97% for Clustal W. MSA-GA with no prealignments performed better than Clustal W on 12 test cases and worse on 16. The number of test cases for each reference set is insufficient to draw conclusions as to the suitability of MSA-GA for any particular class of problems; nevertheless, MSA-GA seems to perform better with short or medium length sequences and with sequences of low identity, which is in close agreement to the results for the iterative method using genetic algorithms implemented in SAGA (Notredame and Higgins, 1996; Thompson et al.,1999a). The orphan sequences in reference 2 seem to bias the alignment, entrapping the GA at a local optimum, which also follow the results from SAGA (Thompson et al., 1999a). MSA-GA scored higher for the tested references in groups 4 and 8, but only in reference 4 did the alignments improve by more than 2%. MSA-GA with seeded prealignments improved on the original Clustal alignments in 17 test cases. Of these, six improved the alignment by more than 2%. The average improvement was 1.32%, which closely agrees with the average 1.6% improvement obtained with iterative approaches applied to Clustal W alignments (Wallace et al., 2005). Even though Notredame and Higgins (1996) observed that seeding could entrap the GA at a local optimum, our results suggest that better solutions can be found if a run is seeded with prealignments. Of the 28 test cases, in only three the GA did not change the original alignment score. In seven cases, the BaliScore value did not change, but in four of these the fitness value in MSA-GA increased. Similar results were obtained by Thomsen and Boomsma (2004) seeding Clustal W alignments into SAGA, with these outperforming randomly initiated alignments. The remaining four alignments yielded worse results than Clustal W even though the fitness values increased, which indicates that the objective function does not adequately map to the ‘biological’ alignment. An example of this effect was found in 1idy in reference 1. In an MSA-GA run, the sum-of-pairs score of the Clustal prealignment was 641 and 655 at the end of the run, which yielded a worse BaliScore value (0.521-0.438). More interestingly, the score for the BaliBase alignment itself is 659, clearly demonstrating the non-linear relation between the fitness score and the ‘biological’ alignment. Further, the MSA-GA score without a prealignment evolved to a final value of 663 (BaliScore 0.427), beyond the theoretical ‘global optimal’ value.
DISCUSSION AND FUTURE PERSPECTIVES Genetic algorithms are computationally expensive, which hinders their mainstream adoption as a tool for multiple sequence alignments. On the other hand, the clear distinction between the scoring scheme and the GA itself makes them particularly well suited for testing or implementing different objective functions. The inadequacy of the scoring methods for certain types of alignments is a well-known problem and is an active field of research in MSA. MSA-GA without prealignments yielded better results than Clustal in 43% of the test cases and worse in the remaining, with the alignments on average 4% inferior. These results do not suggest that MSA-GA, even ignoring the time demand, is a superior alternative to Clustal W. Nevertheless, MSA-GA can be used as an additional tool to generate a second alignment from which the researcher can select the best alignment. Alternatively, the alignments produced by Clustal can be used to seed the MSA-GA alignments. For this scenario, the results from the test cases improved the original Clustal alignments in 61% of the cases and were worse in only 14% (in 3 alignments 2% or less worse and 8.3% in one alignment - the 1idy reference, mentioned above, for which the objective function and the ‘biological alignment’ do not seem to relate well); for the remaining 25%, the alignment did not change. The average improvement was 1.32% and the best almost 15% better. Depending on the application of the alignment, even small gains can justify the time expense. A further aspect of MSA-GA is that it allows any type of prealignment and weights to be used. This means that the initial population can be seeded with a prealignment not only from Clustal but also from other MSA programs or, more interestingly, from structural databases. MSA-GA with prealignments was superior to MSA-GA without prealignments in 71% of the cases. In the eight cases where the latter performed better, MSA-GA with prealignments also improved the original alignment, but to a lesser degree. This is possibly due to entrapment at a local optimum as a result of the seeding. A last consideration is the importance of GA parameter settings. MSA-GA seems to be sensitive to changes in these settings. Changes in population size, mutation and recombination rates and tournament size affect the final alignment and converge times. We performed a series of long runs with kinase in reference 1 changing the GA parameters (data not shown). BaliScore results were in the range 0.201-0.492. This provides evidence of the stochastic nature of the GA, which can be a matter of concern for the user. These settings are still empirically defined, with no theoretical framework for defining the best settings. SAGA uses a complex operator scheduling to try to optimize the parameters during run time, but unfortunately, the results of Thomsen and Boomsma (2004) demonstrated that there was no significant difference with or without operator scheduling. In summary, our results indicate that the GA seeded with prealigned sequences can improve the alignments derived from Clustal W. MSA-GA without prealignments is less guaranteed to find the best alignment, and the stochastic nature of results can render the approach impractical for daily usage. MSA-GA is computationally expensive, as evidently, an iterative approach cannot compete in terms of speed with a progressive method. However, more importantly, the main motivation behind this study was to develop a general framework for testing and implementing different scoring functions. We have shown that a simple GA is capable of optimizing an alignment without the need of excessively complex operators and the approach used in MSA-GA makes extending and/or replacing objective functions a trivial task. As noted before, an advantage of an evolutionary algorithm approach in which the objective function is disjointed from the optimization method is that extra components can be easily added to the objective function. Consider for example, if relatively large regions (e.g., >100 bp) have been duplicated, probably as a single event, this should not have a dramatic effect on scores, at least for some applications such as phylogeny. Including this and other such events (e.g., inversion) in a strong-arm optimization method would be highly complex, but with an evolutionary algorithm any type of feature or constraint on solutions can be targeted - features that we may not anticipate until appropriate problems prevail. Prior adoption of an evolutionary algorithm will make such hurdles much easier to overcome. Future study includes extending the available set of scoring matrices and implementing a function for user-defined matrices. We also want to include different scoring schemes in MSA-GA as the consistency-based objective functions COFFEE (Notredame et al., 1998) and T-COFFEE (Notredame et al., 2000) and the recent Log Expectation scoring function (Edgar, 2004). Further studies are needed to test the best scope of application for the GA and to evaluate if it is getting entrapped at local optima with longer sequences or alignments with many sequences, as these initial results seem to indicate. This may require the development of specific operators in the GA. ACKNOWLEDGMENTS Research supported in part by the University of New England and the Cooperative Research Centre for Cattle and Beef Quality (Beef CRC). REFERENCES Altschul SF (1989). Gap costs for multiple sequence alignment. J. Theor. Biol. 138: 297-309. Anbarasu LA, Narayanasamy P and Sundararajan V (2000). Multiple molecular sequence alignment by island parallel genetic algorithm. Curr. Sci. 78: 858-863. Atmar W (1994). Notes on the simulation of evolution. IEEE Trans. Neural Networks 5: 130-147. Bäck T, Fogel DB and Michalewicz T (2000). Evolutionary computation 1: basic algorithms and operators. Institute of Physics Publishing, Bristol. Bahr A, Thompson JD, Thierry JC and Poch O (2001). BAliBASE (Benchmark Alignment dataBASE): enhancements for repeats, transmembrane sequences and circular permutations. Nucleic Acids Res. 29: Bellman RE (2003). Dynamic programming. Dover Publications, Dover. Bonizzoni P and Della Vedova G (2001). The complexity of multiple sequence alignment with SP-score that is a metric. Theor. Comp. Sci. 259: 63-79. Chellapilla K and Fogel GB (1999). Multiple sequence alignment using evolutionary programming. Congress on Evolutionary Computation (CEC99), Washington DC. Chenna R, Sugawara H, Koike T, Lopez R, et al. (2003). Multiple sequence alignment with the Clustal series of programs. Nucleic Acids Res. 31: 3497-3500. Dayhoff MO (1978). Survey of new data and computer methods of analysis. In: Atlas of protein sequence and structure 5, Suppl 3 (Dayhoff MO, ed.). National Biomedical Research Foundation, Silver Springs, 2-8. Durbin R, Eddy S, Krogh A and Mitchison G (1998). Biological sequence analysis: probabalistic models of proteins and nucleic acids. Cambridge University Press, Cambridge. Ebedes J and Datta A (2004). Multiple sequence alignment in parallel on a workstation cluster. Bioinformatics 20: 1193-1195. Eddy SR (1998). Profile hidden Markov models. Bioinformatics 14: 755-763. Edgar RC (2004). MUSCLE: a multiple sequence alignment method with reduced time and space complexity. BMC Bioinformatics 5: 113. Eshelman LJ (2000). Genetic algorithms. Evolutionary Computation 1: Basic Algorithms and Operators. Institute of Physics Publishing, Bristol. Feng DF and Doolittle RF (1987). Progressive sequence alignment as a prerequisite to correct phylogenetic trees. J. Mol. Evol. 25: 351-360. George DG, Barker WC and Hunt LT (1990). Mutation data matrix and its uses. Methods Enzymol. 183: 333-351. Goldberg DE (1987). Simple genetic algorithms and the minimal, deceptive problem. In: Genetic algorithms and simulated annealing (Davis L, ed.). Morgan Kaufmann, San Mateo, 74-88. Gonnet GH, Cohen MA and Benner SA (1992). Exhaustive matching of the entire protein sequence database. Science 256: 1443-1445. Henikoff S and Henikoff JG (1992). Amino acid substitution matrices from protein blocks. Proc. Natl. Acad. Sci. USA 89: 10915-10919. Hirosawa M, Totoki Y, Hoshida M and Ishikawa M (1995). Comprehensive study on iterative algorithms of multiple sequence alignment. Comput. Appl. Biosci. 11: 13-18. Jones DT, Taylor WR and Thornton JM (1992). The rapid generation of mutation data matrices from protein sequences. Comput. Appl. Biosci. 8: 275-282. Just W (2001). Computational complexity of multiple sequence alignment with SP-score. J. Comput. Biol. 8: 615-623. Karplus K and Hu B (2001). Evaluation of protein multiple alignments by SAM-T99 using the BAliBASE multiple alignment test set. Bioinformatics 17: 713-720. Kim J, Pramanik S and Chung MJ (1994). Multiple sequence alignment using simulated annealing. Comput. Appl. Biosci. 10: 419-426. Lipman DJ, Altschul SF and Kececioglu JD (1989). A tool for multiple sequence alignment. Proc. Natl. Acad. Sci. USA 86: 4412-4415. McClure MA, Vasi TK and Fitch WM (1994). Comparative analysis of multiple protein-sequence alignment methods. Mol. Biol. Evol. 11: 571-592. Michalewicz T and Fogel DB (2000). How to solve it: modern heuristics. Springer-Verlag, Heidelberg. Mount WD (2004). Bioinformatics: sequence and genome analysis. Cold Spring Harbor Laboratory Press, New York. Needleman SB and Wunsch CD (1970). A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 48: 443-453. Nguyen HD, Yoshihara I, Yamamori K and Yasunaga M (2002). Aligning multiple protein sequences by parallel hybrid genetic algorithm. Genome Inform. 13: 123-132. Notredame C (2002). Recent progress in multiple sequence alignment: a survey. Pharmacogenomics 3: 131-144. Notredame C and Higgins DG (1996). SAGA: sequence alignment by genetic algorithm. Nucleic Acids Res. 24: 1515-1524. Notredame C, Holm L and Higgins DG (1998). COFFEE: an objective function for multiple sequence alignments. Bioinformatics 14: 407-422. Notredame C, Higgins DG and Heringa J (2000). T-Coffee: a novel method for fast and accurate multiple sequence alignment. J. Mol. Biol. 302: 205-217. Riaz T, Wang Y and Li KB (2004). Multiple sequence alignment using tabu search. Procceedings of the 2nd Conference on Asia-Pacific Bioinformatics. Australian Computer Society, New Zealand, 223-232. Saitou N and Nei M (1987). The neighbor-joining method: a new method for reconstructing phylogenetic trees. Mol. Biol. Evol. 4: 406-425. Sander C and Schneider R (1991). Database of homology-derived protein structures and the structural meaning of sequence alignment. Proteins 9: 56-68. Shyu C, Sheneman L and Foster JA (2004). Multiple sequence alignment with evolutionary computation. Genet. Prog. Evol. Mach. 5: 121-144. Smith TF and Waterman MS (1981). Identification of common molecular subsequences. J. Mol. Biol. 147: 195-197. Stoye J, Perrey SW and Dress AWM (1997). Improving the divide-and-conquer approach to sum-of-pairs multiple sequence alignment. App. Maths. Letters 10: 67-73. Taylor WR (1987). Multiple sequence alignment by a pairwise algorithm. Comput. Appl. Biosci. 3: 81-87. Thompson JD, Higgins DG and Gibson TJ (1994). Clustal W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 22: 4673-4680. Thompson JD, Plewniak F and Poch O (1999a). A comprehensive comparison of multiple sequence alignment programs. Nucleic Acids Res. 27: 2682-2690. Thompson JD, Plewniak F and Poch O (1999b). BAliBASE: a benchmark alignment database for the evaluation of multiple alignment programs. Bioinformatics 15: 87-88. Thomsen R and Boomsma W (2004). Multiple sequence alignment using SAGA: investigating the effects of operator scheduling, population seeding, and crossover operators. Appl. Evol. Comput. 3005: 113-122. Thomsen R, Fogel GB and Krink T (2002). A Clustal alignment improver using evolutionary algorithms. Proceedings of the 4th Congress on Evolutionary Computation (CEC2002), Honolulu, 121-126. Wallace IM, O’Sullivan O and Higgins DG (2005). Evaluation of iterative alignment algorithms for multiple alignment. Bioinformatics 21: 1408-1414. Zhang C and Wong AK (1997). A genetic algorithm for multiple molecular sequence alignment. Comput. Appl. Biosci. 13: 565-581. |
|