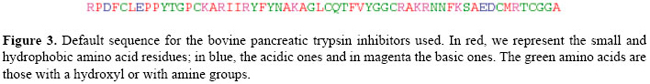Finding protein-protein interaction patterns
by contact map matching
R.C. Melo1,2, C. Ribeiro1,2, C.S. Murray2, C.J.M. Veloso1,2, C.H. da Silveira1,2, G. Neshich3, Genet. Mol. Res. 6 (4): 946-963 (2007) ABSTRACT. We propose a novel method for defining patterns of contacts present in protein-protein complexes. A new use of the traditional contact maps (more frequently used for representation of the intra-chain contacts) is presented for analysis of inter-chain contacts. Using an algorithm based on image processing techniques, we can compare protein-protein interaction maps and also obtain a dissimilarity score between them. The same algorithm used to compare the maps can align the contacts of all the complexes and be helpful in the determination of a pattern of conserved interactions at the interfaces. We present an example for the application of this method by analyzing the pattern of interaction of bovine pancreatic trypsin inhibitors and trypsins, chymotrypsins, a thrombin, a matriptase, and a kallikrein - all classified as serine proteases. We found 20 contacts conserved in trypsins and chymotrypsins and 3 specific ones are present in all the serine protease complexes studied. The method was able to identify important contacts for the protein family studied and the results are in agreement with the literature. Key words: BPTI, Protein-protein interactions, Contact maps, Serine proteases INTRODUCTION Genome projects have revealed novel genes for various model organisms. However, for the vast majority of the genes, there is a lack of any clue as to their specific function. Even for organisms extensively studied in molecular genetics, almost half of the genes have no known function. In this context, the comprehensive analysis of biomolecules such as mRNAs, proteins and metabolites is very promising. In this study, we focus on the information which could be obtained by the analysis of protein-protein interactions (PPIs). It is well known that specific PPIs are involved in almost all physiological processes. Sensing extracellular signals, for example, is a matter of receptor to adaptor interactions. The shape of the cell is maintained by an intricate network of structural protein interactions. Understanding PPIs involved in common cellular functions is important to get a grasp of how they work cooperatively in the cell, and PPIs are also of extreme importance in providing informative hints about protein function (Ito et al., 2001). PPIs are established based on specific surface features: the main one is the surface complementarity of the proteins that interact as well as the appropriate distribution of residues in the protein-protein surface. When proteins are interacting, many contacts are formed between their amino acid residues to stabilize the complex. In this study, we propose a novel strategy to compare the PPIs of complexes which were crystallized and had their structure solved by X-ray crystallography. The proposed method can, additionally, define patterns of interactions that are essential for complex formation and stabilization. It is well known that contact maps are useful tools for studying protein structures as they can represent them robustly. The traditional contact map is a symmetric square matrix of n × n positions, where n is the number of residues of a protein, and each [i, j] position indicates whether there is a contact between the residues i and j. In a previous study (Melo RC, Fernandes FA Jr., Carceroni RL, Murray CS, et al., unpublished results), we described the protein structure comparison as a problem of measuring the dissimilarity between contact maps. We demonstrated that by using only hydrophobic interactions, hydrogen bonds (the ones which do not include water molecules) and charged attractive contacts, we could classify protein structures with high precision (up to 90% for the tested families). This indicates that we have developed sharp algorithms for contact map comparison and also that contact maps are conserved for a specific fold. In this study, we propose a variation of the contact maps, which shows PPIs (inter-chain) instead of intra-chain contacts. We used the well-studied bovine pancreatic trypsin inhibitors (BPTIs) bound to five types of serine proteases (trypsins, chymotrypsins, thrombins, matriptases, and kallikreins) to test the proposed method. We show that trypsins and chymotrypsins display a specific pattern of contacts with the inhibitor and we also compare these patterns with the contacts of thrombin, matriptase and kallikrein complexes. We found that there is a small set of conserved contacts in all the complexes and that they are essential for BPTI binding according to literature data (Krowarsch et al., 1999; Brandsdal et al., 2001; Wilmouth et al., 2001; Topf et al., 2002; Bobofchak et al., 2005). MATERIAL AND METHODS Contact maps In Figure 1, we present an example of the traditional symmetric square contact map. It is an n × n matrix, where n is the number of residues of a protein chain, and each [i, j] position indicates whether or not there is a contact between the residues i and j. The protein-protein interaction maps We define the PPI map as an m × n matrix in which m is the number of residues of the first protein and n is the number of residues of the other one. Thus, an important difference of contact maps and our PPI maps is that they are not square and symmetrical, for obvious reasons. The point [i, j] indicates whether or not there is a contact between the residue i of the first protein and the j one of the other. The traditional contact maps do not differentiate the nature of the contacts, but we consider the following types of contacts:
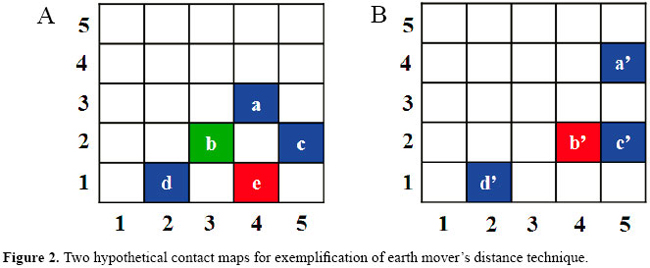
The hydrogen bonds can be formed between the main chain of a residue and the main chain of the other, between main chains and side chains and also side chains and side chains. We also consider the hydrogen bonds with one or two water molecules between the interacting residues. We believe that the inclusion of all contact types is important in order to make the method more precise because interactions between proteins are very specific. The contacts we use were taken from the Blue Star Sting Suite (Contacts Module) described by Mancini et al. (2004). The method used by them to characterize contacts can be found in Sobolev et al. (1999). The map comparison algorithm In a previous study (Fernandes Jr. et al., 2004), we modeled the problem of identifying how close in structure two proteins are as a problem of measuring the similarity between their contact maps. We think that through the type and position of the contacts of a protein, we can classify its fold. In that research, we studied two conceptually distinct computer vision approaches to measure this similarity: one is an image registration algorithm (based on a metric we call average dispersion radius) and the other is a content-based image retrieval technique (which uses the color correlogram). The image registration was more accurate in our experiments. 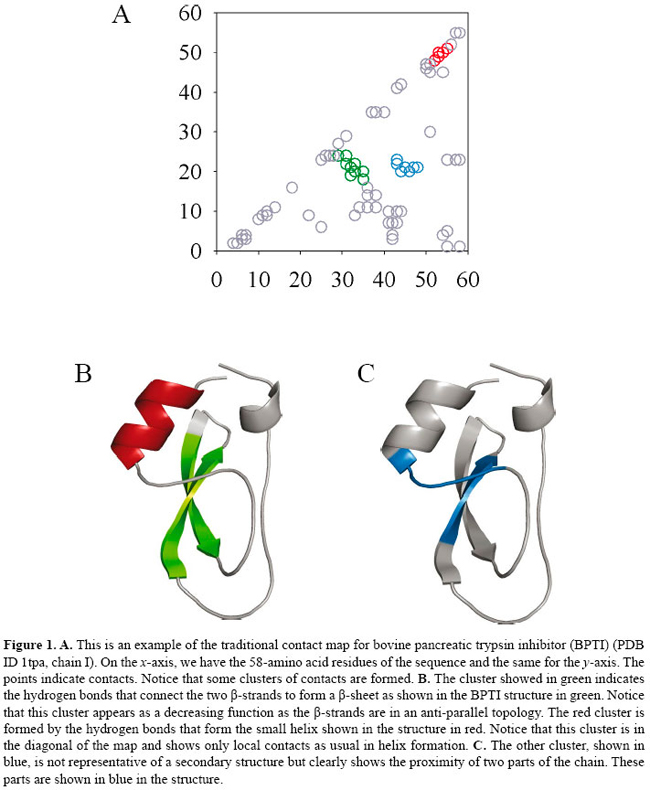 After that research, we developed a new image registration metric for contact map comparison which is based on the earth mover’s distance (EMD) (de Melo et al., 2006). This new algorithm is more accurate than the average dispersion radius. The image registration paradigm (Brown, 1992) is often used to match multiple images as a single object that undergoes non-rigid transformations (Maintz and Viergever, 1998). A cost is attributed to each deformation that the object may undergo and the image-to-image dissimilarity is computed by finding the minimum-cost deformation that maps one image to the other. A motivation to apply this idea to protein contact maps is that distinct proteins did evolve from common ancestral molecules, and their phylogenetic distances are strongly correlated to structural dissimilarity. Thus, if we can somehow model the "deformations" needed to "warp" a contact map into another as a sequence of simple transformations that mimic the effects of evolutionary changes in protein structure, the structural similarity between two proteins may be computed by finding the minimum-cost sequence of such transformations between their contact maps. We have shown that there is a trade-off in the choice between these paradigms: context-based image retrieval techniques tend to be more efficient with very large data sets, but, on the other hand, similarity-based techniques tend to be more accurate, at least in terms of matching pairs of images that are closely related. Thus, we decided to use the algorithm based on the EMD to compare PPI maps as they are very specific for a pair of proteins and two similar complexes show a very similar contact pattern. The use of EMD in image databases was initially proposed by Rubner et al. (1998). The idea is that each contact in one map is treated as a unit of mass of earth spread in a space on which a ground distance is given and the contacts in the other map are treated as holes with unit capacity in the same space. The EMD measures the amount of work needed to fill the holes with earth under the constraint that masses of a given type of contact may only be used to fill up holes with the same type. As noted by Rubner et al. (1998), computing EMD is equivalent to solving the transportation problem, which is a very well-known linear programming problem. More specifically, the EMD is obtained by finding a set of non-negative earth flows that minimize the earth mover’s total work. Consider the two hypothetical contact maps shown in Figure 2. Imagine that the map A is of the first protein and the map B is of the other protein. Both proteins have 5 residues in this case. The EMD consists of trying to move the colored points of map A to points of the same color of map B with the minimum work. The work is the distance of the movement. First, we will consider the point a of map A. If we compute its Euclidean distance to all the other blue points of map B, we find that a’ and c’ are the closer ones. However, c’ is in the same place as c, so we move a to a’ and store the cost of doing such movement, which is √[(xa-xb)2+(ya-yb)2] = √[(3-4)2+(4-5)2] = 1.41, where xa is the x coordinate of point a in the matrix A, ya is the y coordinate in the same matrix and xb and yb are the coordinates for the image B. Point c will be moved to c’ and d to d’ with 0 cost. Let us now consider the red point e. This particular point will be moved to b’ with cost 1. The green point b does not have a correspondent in map B; thus, we attribute an arbitrary cost of 3 because of this mismatch. Thus, the cost of transforming map A in map B is 5.41. We divide this sum by the total number of contacts which is 9, and the average movement of each point is 0.60 which is the dissimilarity of the two maps.
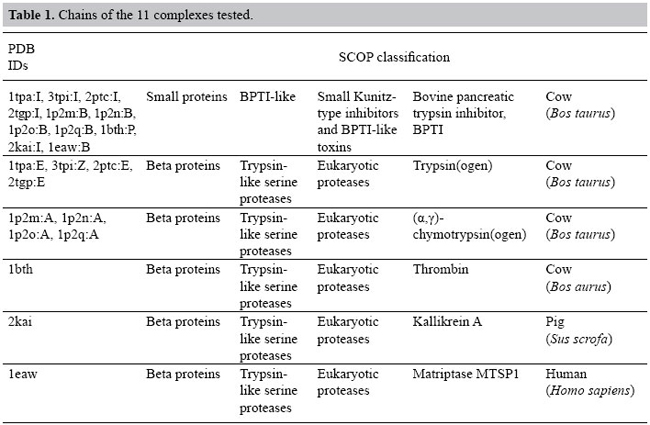
How to align contacts Once we have computed the EMDs of each pair of PPI maps, we aligned the contacts of their maps. For that, we use the earth flows given by the models built to compute EMD. If a given contact in the PPI map 1 was moved to a contact in the PPI map 2, we considered that these two contacts align, that is, that they are equivalent in both maps. In the example of the previous section, contact a aligns to a’, b to anyone, c to c’, d to d’, and e to b’. Selection of complexes We decided to study the serine protease family because they are one of the most well-studied proteins that form complexes with other proteins (Fersht and Sperling, 1973; Kraut, 1977; Carter and Wells, 1988; Warshel et al., 1989; Perona and Craik, 1995; Laskowski Jr. et al., 2000; Laskowski Jr. and Qasim, 2000; Bartlett et al., 2002; Hedstrom, 2002). According to SCOP, there are 12 different inhibitors (that bind to serine proteases) with solved structure. We decided to use BPTI because it is the one that shows more complexes in the PDB. BPTI is a protein found in many tissues throughout the body and inhibits several of the serine protease proteins such as trypsins, kallikreins, chymotrypsins, thrombins, matriptases, and plasmins. Their interaction with serine proteases has been widely studied (Hijikata-Okunomiya et al., 1987; Krowarsch et al., 1999; Czapinska et al., 2000; Brandsdal et al., 2001, 2006). These inhibitors usually have a conserved cysteine residue in forming disulfide bonds. BPTI is a monomeric polypeptide containing about 58-amino acid residues. It is characterized by an extremely stable conformation and binds to trypsins with high affinity (Ka in the 1011-1015 M-1 range). This strong inhibition arises primarily from the interaction between LYS15 side chain of the inhibitor and ASP189 of the enzyme at the bottom of the specificity pocket (Helland et al., 1999). We selected all the BPTI chains present in PDB from the SCOP classification (release 1.69, July 2005) (Murzin et al., 1995) and, then, retrieved all complexes that contain those chains from PDB. We found 136 occurrences of BPTI chains in the PDB. We inspected these data manually and obtained 45 complexes of BPTI with other proteins. We then removed the complexes with BPTIs that were not from Bos taurus and obtained 38 complexes. Among those BPTI complexes, there were 29 trypsins, 4 chymotrypsins, 1 thrombin, 1 matriptase and 1 kallikrein, 1 anticoagulant protein, and 1 coagulation factor VIIa. We decided to use only the serine proteases and selected 4 trypsins, the 4 chymotrypsins, 1 thrombin, 1 matriptase, and 1 kallikrein to test our approach and define the pattern of PPIs among the BPTI and various types of serine proteases. The 4 trypsins were randomly selected: one is an anhydrotrypsin (1tpa), two are trypsinogens (3tpi and 2tgp) and one is a β-trypsin (2ptc). All of them were solved at a 1.9-Å resolution and have the same space group (I222). It is important to mention that all the BPTIs bound to chymotrypsins are mutants (K15G, K15L, K15V, K15F). Due to the lack of data for BPTI complexed with non-trypsin serine proteases, we had to include only the 4 mutants of BPTI complexes with chymotrypsins. They are K15G-M52L, K15L-M52L, K15F-M52L and K15V-M52L from the 1p2m:B, 1p2n:B, 1p2q:B, and 1p2o:B, respectively. Notice that there are 2 mutations in the sequences: residue 15 is an LYS in the wild-type BPTI and is mutated to GLY, LEU, PHE, and VAL. This is an important mutation to consider as LYS15 is located in the center of the canonical binding loop of BPTI and is responsible for up to 50% of all contacts made between the inhibitor and a protease at the interface (Helland et al., 1999). The position 52 can be an MET or an LEU, but it is located in the BPTI helix which is not part of the binding site. Table 1 shows the chains of the complexes used in our experiments.
As can be seen in Table 1, we tried to analyze the interactions of one inhibitor with a set of serine proteases. The inhibitor chains we have collected in our dataset have the following amino acid sequence (Figure 3):
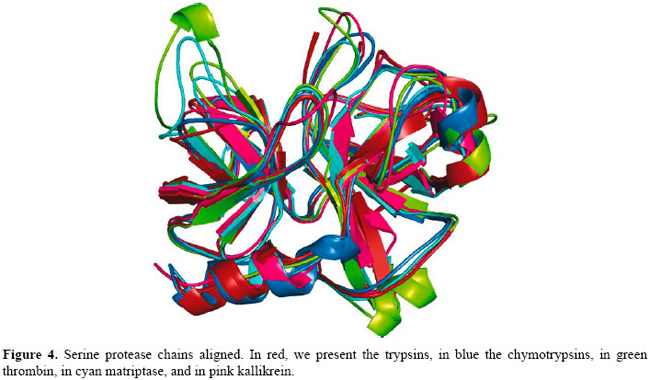
In Figure 4, we present the multiple structure alignment of the serine proteases used in our experiments.
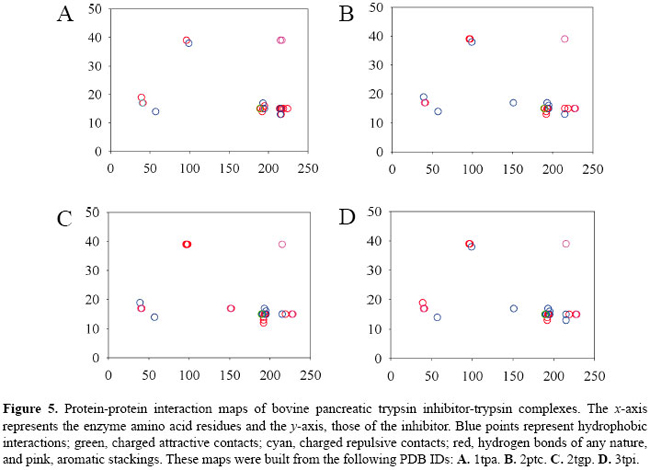
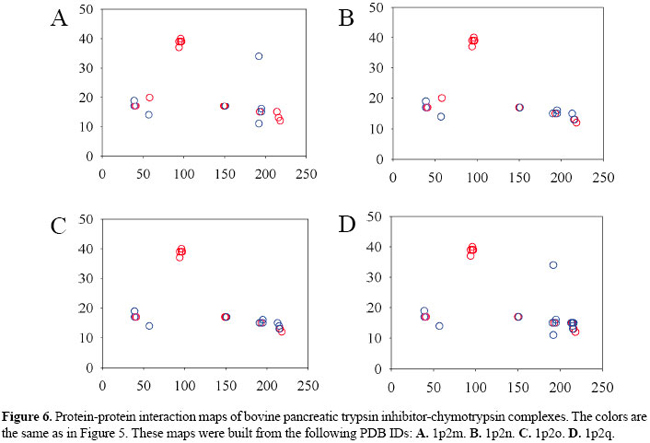
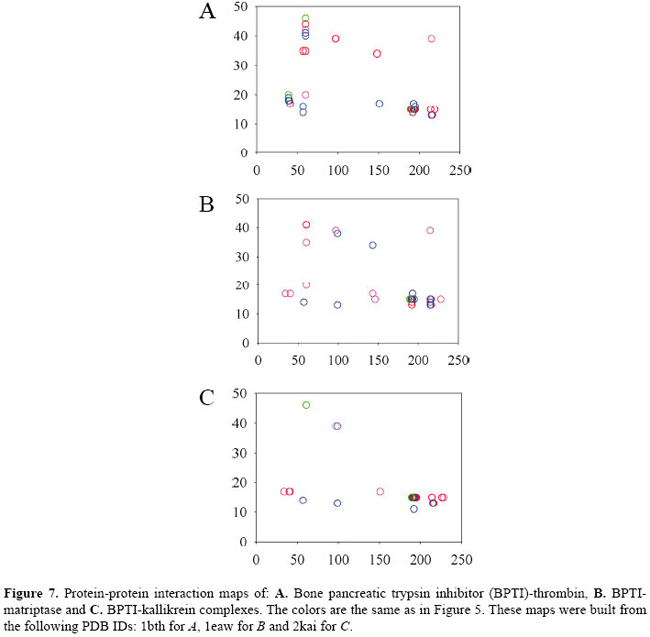
RESULTS AND DISCUSSION Protein-protein interaction maps for the bovine pancreatic trypsin inhibitor-serine protease complexes We built the contact maps for the 11 BPTI-serine protease complexes. By inspecting only those contact maps, it is possible to notice some pattern of interaction of BPTI with trypsins (Figure 5) and with chymotrypsins (Figure 6). We can also see that the complexes with thrombin, matriptase and kallikrein show different patterns of contacts.
We can see that amino acid residues in the inhibitor sequence range 10 to 20 generate the majority of contacts which lock the inhibitor to the enzyme. This happens because the reactive loop of the inhibitor is considered to be formed by residues 12 to 18. We can also see that there are 3 main clusters of contacts: the left one which is next to residue 50 of the enzyme and the other two around residue 200. The denser cluster is the one which shows the contacts originating at residue 15 of the inhibitor and going toward the neighborhood of residue 195 of the enzyme. LYS15 of the inhibitor is the central residue of the reactive loop. It binds to the specificity pocket and mimics a possible substrate, a residue of ARG or LYS. SER195 is part of the catalytic triad and participates directly in the cleavage of the susceptible peptide bond of the substrate. We can identify clusters of contacts in the BPTI-chymotrysin complexes that are quite similar to the complexes of BPTI-trypsins. However, the left cluster of residue 15 of the inhibitor is formed mostly by hydrophobic interactions, and the middle cluster of the same residue is less dense. The upper cluster is much denser, meaning that there is a considerable number of hydrogen bonds between the neighborhood of inhibitor residue 40 and neighborhood of residue 90 of the enzyme. As we can see in Figure 7, contacts in the position of the lower clusters of trypsin and chymotrypsin exist also in the case of thrombin, matriptase and kallikrein. However, there are various other new contacts out of the observable clusters, which indicates that they have a different pattern of interactions. An interesting feature of matriptase is the great number of aromatic stackings that are formed in the BPTI-matriptase interface.
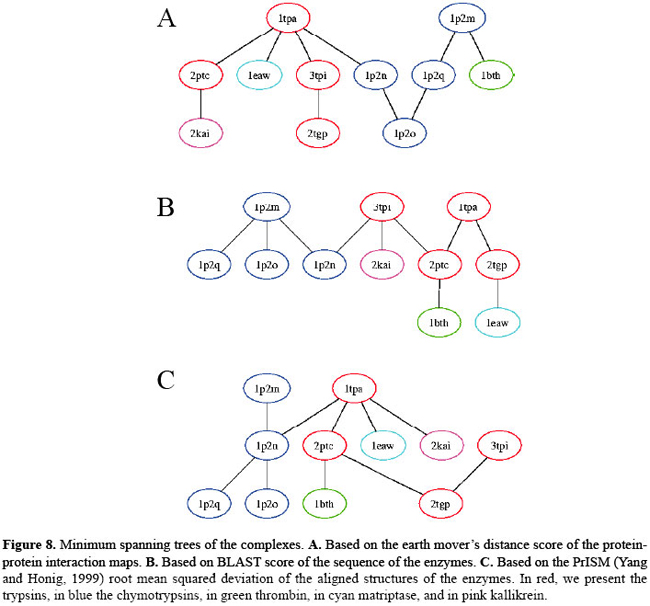
Clustering of complexes using a minimum spanning tree We compared each of the 11 BPTI complex interface contacts with the 10 others using the EMD metric. Similar to Yee and Dill (1993), we have built a minimum spanning tree in which each edge implies similarity between PPIs of the connected complexes. For the present study, a minimum spanning tree is a graph that provides one way to describe relatedness among PPI patterns. Consider a graph in which each of the C complexes is represented by a node. Every possible pair of nodes is connected by an edge. Each edge is weighted by the dissimilarity score relating the two complexes. Hence, we have [C × (C - 1)] / 2 edges. A spanning tree is a sub-graph in which there are only C - 1 edges connecting the C vertices (complexes). In a minimum spanning tree, the sum of the weights of the edges is as small as possible. Thus, the only connectivity is among the most similar complexes. We constructed a minimal spanning tree using Kruskal’s algorithm (Kruskal Jr., 1956). See Figure 8. We can see that, in the EMD tree, complexes of the same type of serine protease are always connected, showing that they were considered to be very similar by the metric. The algorithm was able to associate trypsin complexes as well as the chymotrypsin ones. The trees based on sequence and structure could also cluster the complex of each subfamily. However, we can see that the connections between the items as well as the tree topology change. We converted each tree into a vector and computed the cosine of each pair of vector. We found that the correlation between the trees based on sequence and on structure is 0.37, 0.24 between the trees based on EMD and on sequence and 0.34 between the EMD and structure. The correlation is very small, but as expected, it is greater when comparing EMD with structure than with sequence, as the sequence can vary. However, when the structure remains similar, contacts tend to be much conserved. The correlation between the trees based on sequence and structure is greater than the correlations with the EMD, as expected. When we cluster the complexes in the sequence and structure trees, we use only enzyme data. In the computation of EMD, we also consider inhibitor data, since we use contacts between enzyme and inhibitor.
Conservation of contacts among the complexes Using the flows given by the results of the transportation problem models, we aligned the contacts of the pairs of complexes which were connected in the minimum spanning tree. We analyzed, for the enzymes and inhibitors, the interface-forming residues (IFR) which are the ones which lose accessibility upon formation of a complex. We computed the contacts that each IFR establishes with a ligand and found the preserved ones. For example, the enzyme residue 14 always creates a hydrophobic interaction and residues 193 and 195 always engage in a hydrogen bond. The inhibitor residues 13, 15 and 17 do establish a hydrogen bond in all complexes and 14, 15 and 17 engage in formation of the hydrogen bonds.
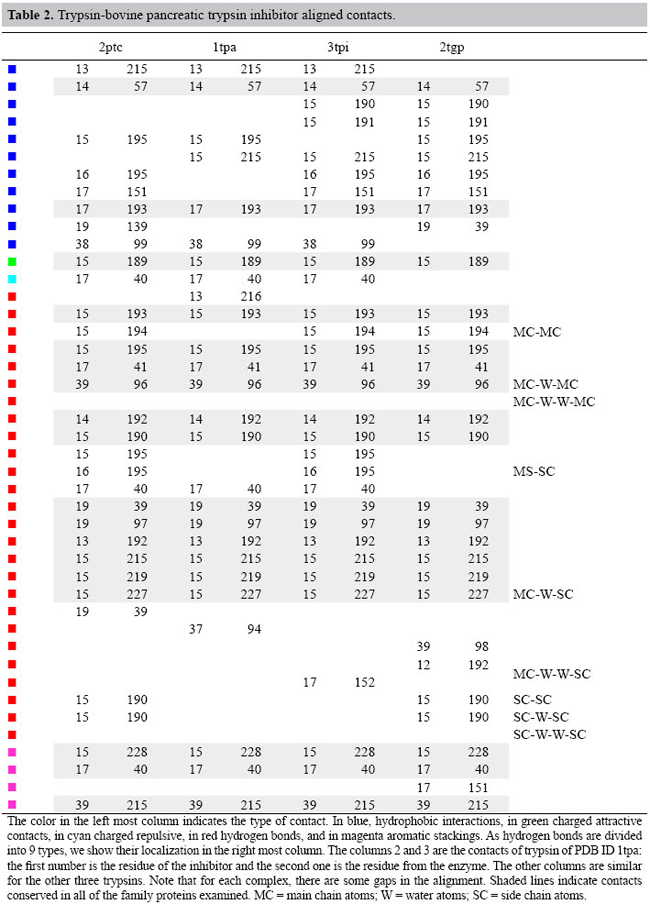
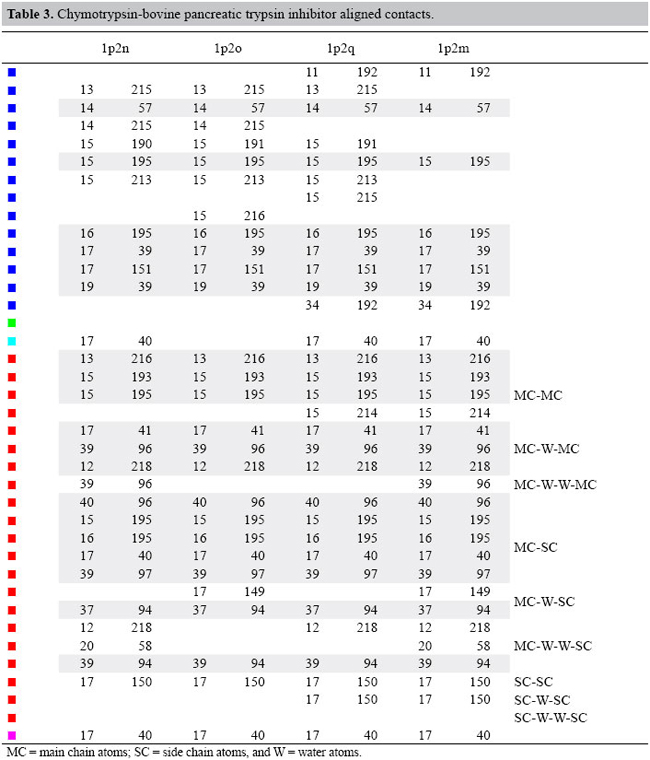
In Tables 2 and 3, we show the alignment of the interface contacts. We can see that there are 18 conserved contacts in the trypsins analyzed: 2 hydrophobic, 1 charged attractive, 12 hydrogen bonds, and 3 aromatic stacking interactions. In chymotrypsins, we have 21 conserved contacts with 6 hydrophobic, 14 hydrogen bonds and 1 aromatic stacking. We can notice that the conserved contacts are quite different between the two types of serine proteases bound to the BPTI. This occurs because the IFRs for the two types of serine proteases are different. Also, we have to consider that the BPTIs complexed with chymotrypsins are mutants (LYS15 changed).
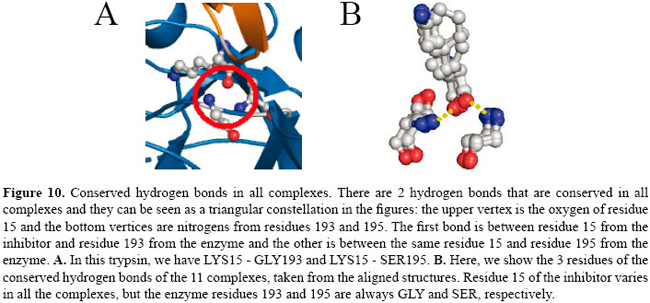
If we compare these contacts with the complexes of thrombin, matriptase and kallikrein, we find only 3 conserved contacts that are co-located in all the complexes. They are a hydrophobic contact between residue 14 of the BPTI and the 57 of the serine protease and two main chain-main chain hydrogen bonds: residue 15 of BPTI with residues 193 and 195 of the enzymes. See Figures 9 and 10.
These two hydrogen bonds are very well known in the literature. After substrate binding to the enzyme, the reaction begins with the hydroxyl group of SER195 making a nucleophilic attack on the carbonyl carbon atom of the substrate. This changes the geometry around this carbon atom from trigonal planar to tetrahedral. The inherently unstable tetrahedral intermediate formed bears a formal negative charge on the oxygen atom derived from the carbonyl group. This charge is stabilized by the hydrogen bonds between main chains of the GLY193 and SER195. The site where these interactions occur in the protein is termed an oxyanion hole. Conservation of the contacts in other serine protease complexes available in PDB The conserved contacts found in our dataset were found in all the BPTI complexes present in PDB. We verified that even in several BPTI mutant complexes, the conserved contact triplet is present in the interface of the proteins. Helland et al. (1999) determined ten complexes formed between bovine β-trypsins and inhibitor residue 15 variants (GLY, ASP, GLU, GLN, THR, MET, LYS, HIS, PHE, TRP). All complexes were crystallized under the same conditions. They found that all the mutant side chains could be accommodated at the primary binding site of the enzyme, and we verified that even with all these mutations, the hydrogen bonds are conserved for these complexes. CONCLUSIONS This paper proposes a novel method for PPI analysis. We did not find any other algorithm which finds the pattern of PPIs in a family of complexes as we propose. We define novel PPI maps that are maps of interactions between two bound proteins and present an algorithm for comparison of these maps. The algorithm is based on the EMD and was solved by the known transportation problem. We also show how this algorithm can be used to align contacts of complex interfaces and to find patterns of interactions for similar complexes. In our tests, we used the well-studied serine protease family and its more common inhibitor, BPTI. We used 11 complexes of BPTI, namely 4 with trypsins, 4 with chymotrypsins, 1 with thrombin, 1 with matriptase, and 1 with kallikrein. We found a pattern that was identified by our procedure in all the complexes of BPTI-serine proteases from the PDB structures present in SCOP. Many studies have been conducted on the interactions of BPTI with serine proteases. The active site of the enzyme is well known as is the inhibition mechanism. It is known that the hydrogen bonds are the most frequent and most important type of contacts that promote binding between these two proteins. In analyzing the contacts present in trypsin, chymotrypsin, thrombin, matriptase, and kallikrein interfaces with BPTI, we identified a set of 18 contacts conserved in trypsins and 20 in chymotrypsins. The experiments show that there is a different pattern of interaction for each subfamily of serine proteases. In comparing the contacts in all the subfamilies, we found 3 contacts that are present in all of them. They are a hydrophobic contact between CYS14 of the inhibitor and HIS57 of the enzyme and two main chain-main chain hydrogen bonds between residue 15 of the inhibitor and residues 193 and 195 of the enzyme. The hydrophobic interaction is formed by conserved amino acid residues: one is a CYS which is conserved because it forms a disulfide bridge in BPTI and the other is HIS57 of the inhibitor which is conserved because it is part of the catalytic triad. In this case, we believe that the contact is conserved because the contact-forming residues are conserved. The two conserved hydrogen bonds are very important and well known in the literature as the oxyanion hole. This site is formed by the backbone N atoms of the catalytic SER195 and GLY193 and engages the backbone O atom of the P1 residue of substrate in an important hydrogen bond interaction (Wilmouth et al., 2001). From kinetic and structural data, Bobofchak et al. (2005) estimate that the hydrogen bond with GLY193 contributes to the stabilization of the ground and transition states of >1.5 kcal/mol but <3.0 kcal/mol. The hydrogen bond with SER15 is also very important in the complex stability and its break was shown to be implicated in the release of the substrate after the cleavage of the peptide bond (Topf et al., 2002). Helland et al. (1999) showed that even when mutating residue 15, which is usually an LYS, with GLY, ASP, GLU, GLN, THR, MET, LYS, HIS, PHE or TRP, the hydrogen bonds are conserved. The results for the tests with serine proteases are not new but are in agreement with data in the literature. We still have to extend the application of our tests to other complexes of known structures, but the method seems to be very promising as the interactions involved in binding between two proteins tend to be conserved for similar complexes, which makes the method very appropriate. REFERENCES Bartlett GJ, Porter CT, Borkakoti N and Thornton JM (2002). Analysis of catalytic residues in enzyme active sites. J. Mol. Biol. 324: 105-121. Bobofchak KM, Pineda AO, Mathews FS and Di Cera E (2005). Energetic and structural consequences of perturbing Gly-193 in the oxyanion hole of serine proteases. J. Biol. Chem. 280: 25644-25650. Brandsdal BO, Aqvist J and Smalas AO (2001). Computational analysis of binding of P1 variants to trypsin. Protein Sci. 10: 1584-1595. Brandsdal BO, Smalas AO and Aqvist J (2006). Free energy calculations show that acidic P1 variants undergo large pKa shifts upon binding to trypsin. Proteins 64: 740-748. Brown LG (1992). A survey of image registration techniques. ACM Comput. Surv. 24: 325-376. Carter P and Wells JA (1988). Dissecting the catalytic triad of a serine protease. Nature 332: 564-568. Czapinska H, Otlewski J, Krzywda S, Sheldrick GM, et al. (2000). High-resolution structure of bovine pancreatic trypsin inhibitor with altered binding loop sequence. J. Mol. Biol. 295: 1237-1249. de Melo RC, Lopes CE, Fernandes FA Jr, da Silveira CH, et al. (2006). A contact map matching approach to protein structure similarity analysis. Genet. Mol. Res. 5: 284-308. Fernandes FA Jr, Lopes CER, Melo RC, Santoro MM, et al. (2004). An image-matching approach to protein similarity analysis. In: Proceedings of the 17th Brazilian Symposium of Computer Graphics and Image Processing, Curitiba, 17-24. Fersht AR and Sperling J (1973). The charge relay system in chymotrypsin and chymotrypsinogen. J. Mol. Biol. 74: 137-149. Hedstrom L (2002). Serine protease mechanism and specificity. Chem. Rev. 102: 4501-4524. Helland R, Otlewski J, Sundheim O, Dadlez M, et al. (1999). The crystal structures of the complexes between bovine beta-trypsin and ten P1 variants of BPTI. J. Mol. Biol. 287: 923-942. Hijikata-Okunomiya A, Okamoto S, Kikumoto R, Tamao Y, et al. (1987). Similarity and dissimilarity in the stereogeometry of the active sites of thrombin, trypsin, plasmin and glandular kallikrein. Thromb. Res. 45: 451-462. Ito T, Chiba T, Ozawa R, Yoshida M, et al. (2001). A comprehensive two-hybrid analysis to explore the yeast protein interactome. Proc. Natl. Acad. Sci. USA 98: 4569-4574. Kraut J (1977). Serine proteases: structure and mechanism of catalysis. Annu. Rev. Biochem. 46: 331-358. Krowarsch D, Dadlez M, Buczek O, Krokoszynska I, et al. (1999). Interscaffolding additivity: binding of P1 variants of bovine pancreatic trypsin inhibitor to four serine proteases. J. Mol. Biol. 289: 175-186. Kruskal JB Jr (1956). On the shortest spanning subtree of a graph and the traveling salesman problem. Proc. Am. Math. Soc. 7: 48-50. Laskowski M Jr and Qasim MA (2000). What can the structures of enzyme-inhibitor complexes tell us about the structures of enzyme substrate complexes? Biochim. Biophys. Acta 1477: 324-337. Laskowski M Jr, Qasim MA and Lu SM (2000). Interaction of standard mechanism, canonical protein inhibitors with serine proteinases. In: Protein-Protein Recognition, the Frontiers in Molecular Biology Series (Kleanthous C, ed.). Oxford University Press, New York, 228-279. Maintz JB and Viergever MA (1998). A survey of medical image registration. Med. Image Anal. 2: 1-36. Mancini AL, Higa RH, Oliveira A, Dominiquini F, et al. (2004). STING contacts: a web-based application for identification and analysis of amino acid contacts within protein structure and across protein interfaces. Bioinformatics 20: 2145-2147. Murzin AG, Brenner SE, Hubbard T and Chothia C (1995). SCOP: a structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol. 247: 536-540. Perona JJ and Craik CS (1995). Structural basis of substrate specificity in the serine proteases. Protein Sci. 4: 337-360. Rubner Y, Tomasi C and Guibas LJ (1998). A metric for distributions with applications to image databases. In: Proceedings of IEEE International Conference on Computer Vision, Bombay, 59-66. Sobolev V, Sorokine A, Prilusky J, Abola EE, et al. (1999). Automated analysis of interatomic contacts in proteins. Bioinformatics 15: 327-332. Topf M, Várnai P and Richards WG (2002). Ab initio QM/MM dynamics simulation of the tetrahedral intermediate of serine proteases: insights into the active site hydrogen-bonding network. J. Am. Chem. Soc. 124: 14780-14788. Warshel A, Naray-Szabo G, Sussman F and Hwang JK (1989). How do serine proteases really work? Biochemistry 28: 3629-3637. Wilmouth RC, Edman K, Neutze R, Wright PA, et al. (2001). X-ray snapshots of serine protease catalysis reveal a tetrahedral intermediate. Nat. Struct. Biol. 8: 689-694. Yang AS and Honig B (1999). Sequence to structure alignment in comparative modeling using PrISM. Proteins 3: 66-72. Yee DP and Dill KA (1993). Families and the structural relatedness among globular proteins. Protein Sci. 2: 884-899. |
|